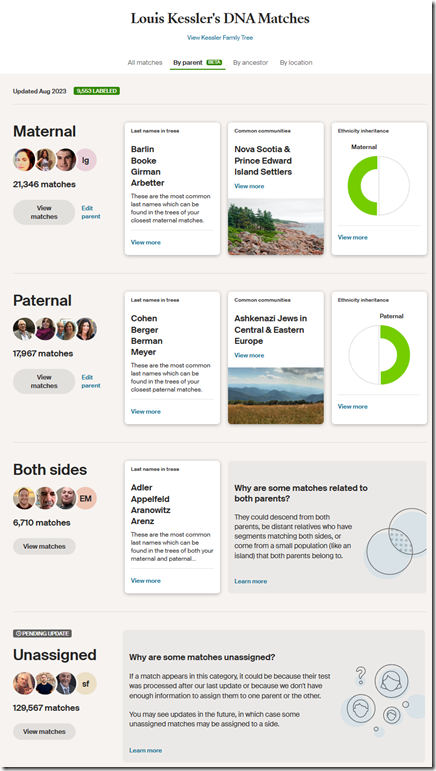
Part of the work of genealogists in this digital age is to scan their old physical material. I’ve got many boxes in the closet and basement as well as binders in my shelves that still need to be gone through and digitized.
You can only do this one piece at a time, so it’s a manner of picking a project and working through it. Then going to the next.
4 Binders of Emails
One of the boxes I went through had a few dozen loose emails from genealogical correspondence that I had printed and meant to file one day. I was actually surprised to find these, because I had 4 binders of printed emails in my bookshelf, and I thought I had already filed them all into these binders.
Since December 2002, I have retained all my emails related to my personal genealogical research in a “Correspondence Genealogy” folder on my Windows computer in Outlook. Between then and now, I have been able to transfer my emails from computer to computer as I upgraded. In total I currently have 9,786 emails in that folder which works out to close to 500 a year.
But from 1995 to 2002, what I used to do was print out my research-related emails and I filed them into 4 binders.

Even if it was a larger photo, it would be hard to read what the faded labels say, but they say:
- G1A1a – My Genealogy Correspondence A-K
- G1B1b – My Genealogy Correspondence L-Z
- G1B2 – My Genealogy Correspondence (Unconnected) 1 of 2
- G1b2 – My Genealogy Correspondence (Unconnected) 2 of 2
The G1 numbering is part of my own genealogical file numbering system. I didn’t even notice the inconsistent numbers I had on these 4 binders until I wrote them above for this article. They should have been G1B1a, G1B1b, G1B2a and G1B2b.
Each binder contains my research correspondence with about 100 people I denote the start of each person with a tab divider that is simply one of those post-it-notes that come in pads. I find they work very well and you can get them in various colors. I don’t use the colors to denote anything. I just like the variation as opposed to them all being yellow.

Each tab lists the name of the person I corresponded with and below that is the family surname(s) and/or place(s) that the conversation was relevant to. Any person had between 1 and 30 printed emails during 1995 to 2002. So this would total another 2,000 emails or so that I received/sent during those years.
About half of those (the first two binders) are from people that are in my tree and I know how I’m connected to, and the last two binders are people that are researching the same surnames or places as me, but who as of yet are unconnected.
My Digitization Equipment
I thought it worthwhile to document the process I use. Someone may find it interesting or useful.
First thing of course, is the equipment. Since these are all printed emails on standard 8.5 x 11 inch paper, the best tool is a sheet feed scanner.
My current scanner is the Epson ES-580W. It’s about $500 and scans at 35 pages per minute.

It fits nicely on my desk and folds up nicely to be out-of-the-way when I’m not using it.
My previous scanner was a higher model Epson DS-860 costing $800 that scanned at 65 pages per minute, but as you’ll see below, it’s not the scanning speed that slows the work. It worked fine for about 5 years. A few years ago, it started occasionally adding lines to my scans, so I had to replace it.
The scanner comes with Epson ScanSmart software which works well enough for me.
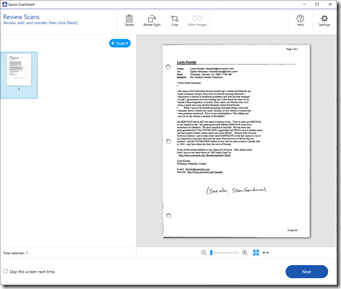
The most important thing to me is that the software can save to Searchable PDF format. That way, I can use Windows to search all my saved PDF scans to find documents with specific words in them.
My Digitization Process
These are the steps I take:
- Select all the emails with one person denoted by a post-it-note and take them out of the binder.
- They were sorted by date with most recent on top, so I reverse the order so that the earliest is first.
- Place the first email from the group in the scanner sheet feed.
- On the scanner, select 1-Sided or 2-Sided (don’t have to select if it is the same as the previous scan) and press “Start”

- The ScanSmart software opens and I can review that the page scanned okay. I then press “Next”.
- Up comes a Window that says “Select Action” and I press “Save”.
- Up comes a window that says “Save to Computer Settings” which I have set to “Searchable PDF” and I press “Save”.
- I repeat steps 1 to 7 for each email with this person.
- The searchable PDF files were all saved to my Documents folder as “scan_nnnn.pdf”.
- I have my Documents folder sorted by latest date, so the scanned files will appear at the top:
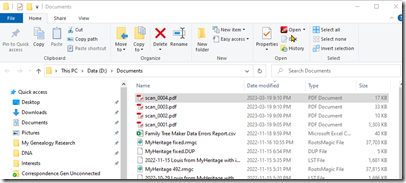
- I have two folders for these emails named “Correspondence Gen Connected” and “Correspondence Gen Unconnected”. In the appropriate folder, I click on the “New folder” button to create a new folder.
- I rename the folder with the person’s name and in parenthesis the surnames and/or places that the emails pertain to. This will be the same information that was on the sticky note. e.g. “Clyde Hertzman (Hertzan)”. I sort of like putting the person’s given name first, but I assume most people will put the surname first.
- I open up the person’s folder and move the 4 scanned emails from the Documents folder window into this folder.
- I now rename each of the files with the date in yyyy-mm-dd format followed by the “type” followed by the subject line of the email. The type can be “email” if the email was from the person to me, “reply” if the email was from me to the person, or “message” if the email was from the person to a genealogy mail list or forum. e.g.:

- I drop the original printed emails and post-it-note for this person into my recycling bin that’s next to my desk.
- Now I repeat steps 1 to 15 for the next person.
This works well enough for me. Each person will take between 1 and 3 minutes to do depending on the number of emails.
Of course this will be slowed down further since I’m re-reading these 25 year old emails as I go and looking to see if there is relevant information that didn’t connect to my tree back then, but does connect to my tree now, 25 years later.
I find with this rechecking, that every so often, I get to add new information to my tree for people that I did not have in my tree back then but do now. In addition, several of these “unconnected people” back then are connected now and I’m sending out an email (when I can find them, since the email is rarely the same after 25 years) to let them know of the new connection.
These rabbit holes add time to the scanning process, but are so much fun and make the whole process worthwhile. Just scanning for scanning’s sake doesn’t cut it.
Summary
On average, in 1 to 3 hours each day I’ve been able to go through about 15 people. One binder has taken me a week. I figure I’ve got another 3 weeks to go to do the other three binders.
I’ll end up with two folders on my computer, one for connected people and one with unconnected people, containing about 400 people subfolders with about 2,000 emails in them.
All the emails are searchable PDF files. Here’s what a Windows search in File Explorer looks like:
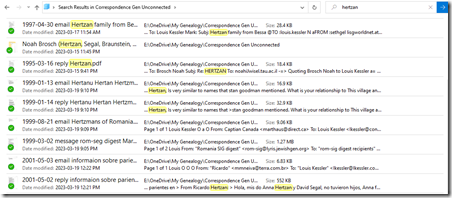
In three weeks when I’m done with this project, I’ll pick my next one. And I’ll have 4 less binders on my bookshelf.











 Feedspot 100 Best Genealogy Blogs
Feedspot 100 Best Genealogy Blogs




