Okay. Let’s do what we did last post for autosomal this time for the X chromosome.
I’ll assume you already know the unique pattern of how the X chromosome get’s passed down, where males get their one X from their mother and females get one of their Xs from their mother and the other from their father. The mother’s is from both of her parents and since the X chromosome (according to FamilyTreeDNA) is 196 cM, that means it recombines with an average of about 1.96 crossovers, which I will round to be 2.. The father’s is passed intact only to his daughter without recombining.
So a son only gets one X chromosome from his mother which will have on average 2 crossovers. A daughter gets one from her mother with 2 crossovers and one from her father with zero crossovers.
This is interesting. That means is a 50% chance of 2 crossovers if it is a son, and that leaves a 25% chance of 2 crossovers and a 25% of zero crossovers if it is a daughter. That works out to 75% chance of 2 and 25% chance of zero giving an expected value of 1.5 crossovers per generation.
And that seems to make sense, since if you got up the female line via mother-mother-mother-mother…, you’ll get 2 crossovers each generation.If you go up the most possible male line which is father-mother-father-mother…, you’ll get zero,2,zero,2,… crossovers which average 1 crossover each generation. So 1.5 seems like it could very well be the average over all lines.
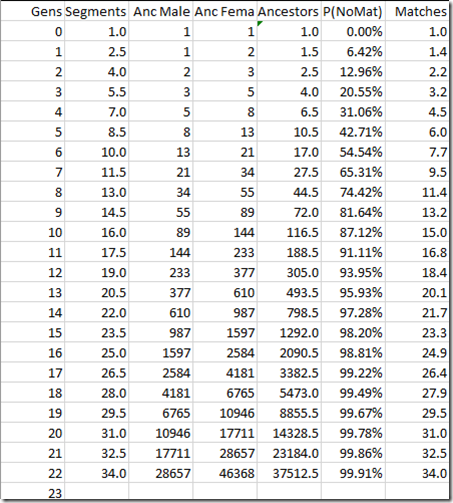
For autosomal, we started with the 23 chromosomes pairs and increased them by 34 segments each generation since both pairs total about 3400 cM. Here for the X chromosome, we’ll start with 1 and increase by 1.5 segments per generation. It’s okay if we use fractional segments here because we’re dealing with averages.
For autosomal, we doubled the number of ancestors each generation. The X chromosome grows not by doubling, but via a Fibonacci sequence. As a lover of mathematics, I must say it’s nice to get good old Fibonacci into DNA. A Fibonacci sequence starts with 1 and 1 and then the next number is always the sum of the previous two, so it’s 1, 1, 2, 3, 5, 8, 13, 21,… A male starts with one X chromosome parent, whereas a female starts with two, so they are offset with one another and an overall average can be taken.
Now lets put the generational levels together:
There you see the segments growing 1.5 per generation, the male and female Fibonacci sequences and their average that represents the expected number of ancestors.
The “P(NoMat)” column is the probability of no segments matching a specific ancestor given that there are N ancestors and S segments and is calculated as:
(1 – 1 / N) ** S
Finally, we can work out the expected number of ancestors that match on the X chromosome by multiplying the number of Ancestors by the probability of matching (which is 1 – the probability of not matching). For higher generations, this number is the same as the number of segments, because it is very unlikely that such a distant ancestor will contribute more than one segment each.
N * P(NoMat)
What this table says is that after 13 generations of X chromosomes, you will have on average 20.5 segments. 95.93% of the 493.5 possible X ancestors will not contribute meaning the 20.5 segments come from 20.1 ancestors, so there is still a chance one or two of them may contribute more than one segment.
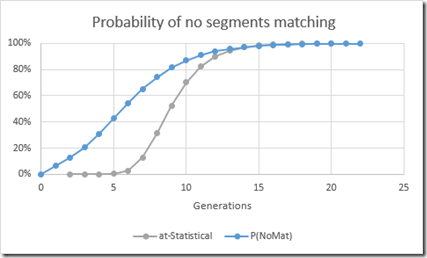
Comparing the probabilities of not matching with autosomal is interesting:
With autosomal, it takes 9 generations before there’s less than a 50% chance that an ancestor won’t pass you a segment. For the X chromosome, it only takes 6 generations for less than a 50% chance. And there’s even a small chance that you won’t inherit an X-segment after 1 generation. This could happen if the X chromosome from the mother’s side has no crossovers and comes from just one of her parents. See the section: The X Doesn’t Recombine as Expected.
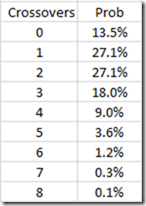
Back to statistics: The Poisson distribution can approximate the number of crossovers per generation. Assuming we are talking about the mother’s X chromosome which has an average of 2 crossovers, a Poisson distribution wiith mean of 2 can give a reasonable estimate of the expected chance of each number of crossovers in one generation on the X chromosome:
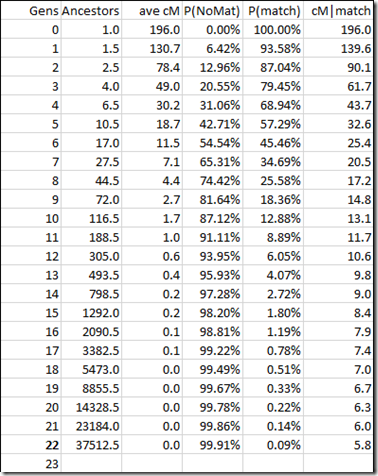
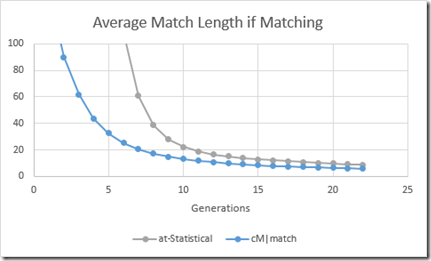
One thing left to do. Like we did for autosomal in my last blog post, we also want to determine the average segment length of a match. So we get this:
Comparing average segment length of an autosomal match with that of an X chromosome match (above) gives:
This shows that autosomal matching segments at any generation are on average a bit longer than X chromosome matching segments.
So now I have everything I need to program this into Behold. Behold will be working with the actual ancestors and know whether it’s a male or female and will take this into account. This will enable Behold to give more accurate information than what I’ve shown above which are just averages. Also, Behold will correctly add the probabilities and compute the expected lengths when there’s pedigree collapse and one ancestor is an ancestor on multiple sides. This should be really useful information that I don’t believe is available anywhere else.
My calculations and assumptions above and in my previous post are as far as I can tell, correct for the averages. I would love to get these two posts peer-reviewed by some genetic genealogists and/or genetic researchers. With encouragement, I could turn these posts into a submission for a publication like the Journal of Genetic Genealogy. I’d be happy to have any problems pointed out and will make any clarifications or corrections that are necessary.